Derivative
Prerequisites Limits
Rate of change of function.
Let \(f\) be a function of \(t\). At \(t=4, f(t)=10\). At \(t=7, f(t)=28\). The Average value of \(f\) at the interval \([4, 7]\) is \((10 + 28)/2 = 19\). But the Average rate of change of \(f\), e.g. how fast/slow it has been changing on the interval, is \(\frac{f(7) - f(4)}{7 - 4} = 18/3 = 6\). It means that function’s value has been increasing at a rate \(6\) units of \(f\) per unit of \(t\). Of course this rate can be negative. The Average rate of change on an interval is the slope of the Secant line that crosses the function at the interval’s boundaries. \[\text{Average rate of change} = Slope_{secant} = \frac{f(a) - f(b)}{a - b}\]
The Average rate of change
Derivative definition
The Average rate of change gives the interval’s rate. The rate of change in a point is called the instantaneous rate of change and it is the Derivative of function in that point. The Derivative of function \(f\) of argument \(x\) in point \(a\) is the instantaneous rate of change of this function in \(a\). It is denoted as “\(f\) prime of \(a\)”: \[f'(a) = Slope_{tangent} = \lim_{x \to a} \frac{f(a) - f(x)}{a - x} = \lim_{\Delta x \to 0} \frac{f(a + \Delta x) - f(a)}{\Delta x} \] As you can see we get the derivative when we start calculating the Average rate of change on less and less intervals. Mathematically it means the limit of average rates of \(f\) in point \(a\). Physically it is the velocity of \(f\). Graphically it is the slope of the tangent line in \(a\). The Tangent line is a line (linear function) that approximates function in the point. For a linear function the tangent is the function itself.
Notations
\[f'(x) \text{ - Newton notation} \] \[\frac{df}{dx} = \frac{d}{dx}f \text{ - Leibniz notation} \] \(d\) stands for the limit of \(\Delta\). Leibniz at a point is \(\frac{df}{dx}|_{x=a}\). Newton at a point is \(f'(a)\).
Derivative graphs
Function graph
Sketch of function's derivative graph
Derivative graphically
How to graph Derivative function
Derivative calculation
By definition for example \(x^2\) \[ \forall a, f'(a) = \lim_{x \to a} \frac{f(x) - f(a)}{x - a} = \lim_{x \to a} \frac{x^2 - a^2}{x - a} = \lim_{x \to a} x + a = 2a \] Linear combinations \[f'(x) = g'(x) + h'(x), f(x) = g(x) + h(x) \] \[f'(x) = Kg'(x), f(x) = Kg(x) \] General power rule If \(n\) is any fixed number and \(f(x) = x^n\). (For integer \(n\) we can prove by definition. Some factorization is required. For any number \(n\) we would need logarithmic differentiation) \[f'(x) = nx^{n-1}\]
Derivative geometrically
Second Derivative
\[f''(x) = f^{(2)}(x) = \frac{d}{dx}(\frac{d}{dx}f) = (\frac{d}{dx})^2(f) = \frac{d^2f}{dx^2} \]
Physically it is the acceleration of \(f\). Graphically it determines the concavity of function.
\(f''<0\), concave down
\(f''>0\), concave up
Inflection points are points where the graph of a function changes “concave up” <=> “concave down”.
Derivative combinations
Product/Quotient. If \(h=g \cdot f\) then by definition \[\frac{\Delta h}{\Delta t} = \frac{(g + \Delta g)(f + \Delta f) - gf}{\Delta t} = \frac{f\Delta g + g\Delta f + \Delta g \Delta f}{\Delta t} = fg' + gf', \Delta t \to 0\] The same applies for the quotient \(h=\frac{g}{f}\)
Product area \(h=g \cdot f\)
Composition
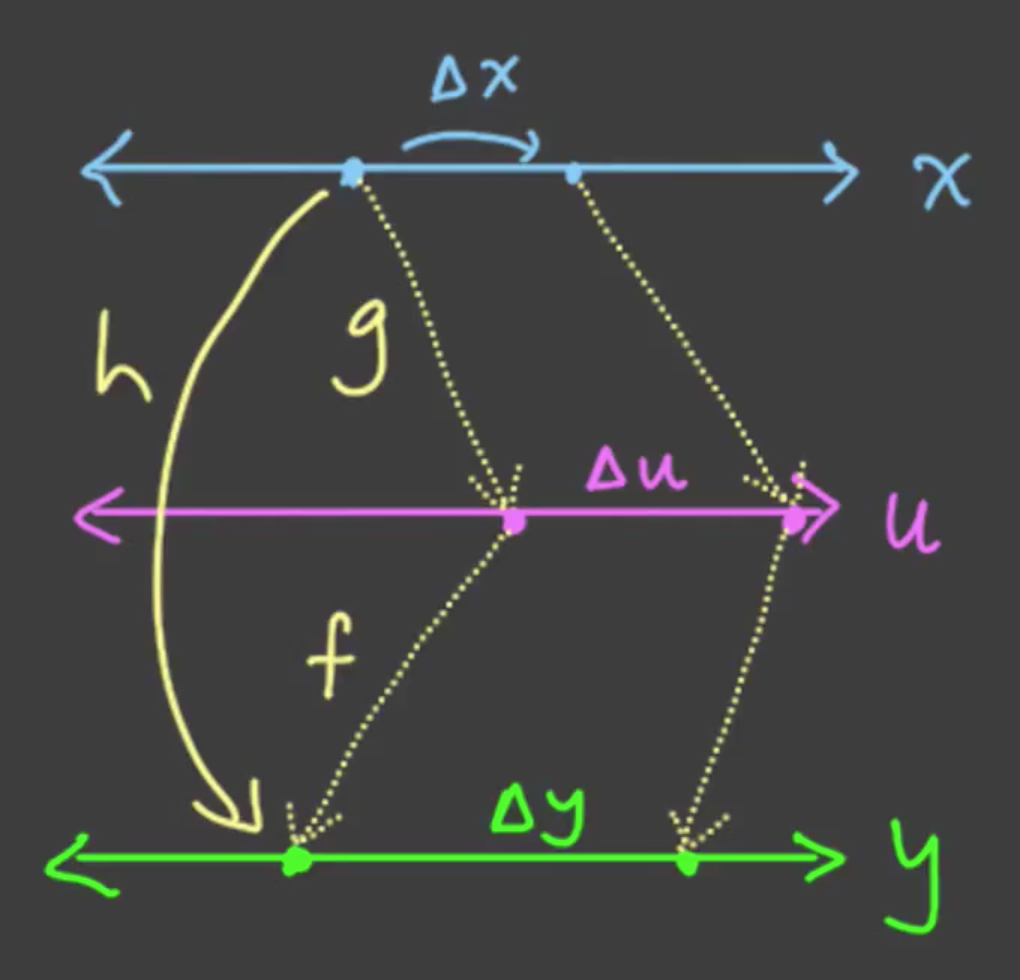Derivative composition
When \(h(x) = f(g(x)) \implies h'(x)=f'(u)g'(x)\) \[f'=\frac{\Delta y}{\Delta u}, g'=\frac{\Delta u}{\Delta x}, h'=\frac{\Delta y}{\Delta x}\] Just make replacements at the above it is our prove. The same can be done through the limit definition.
Chain rule and composition
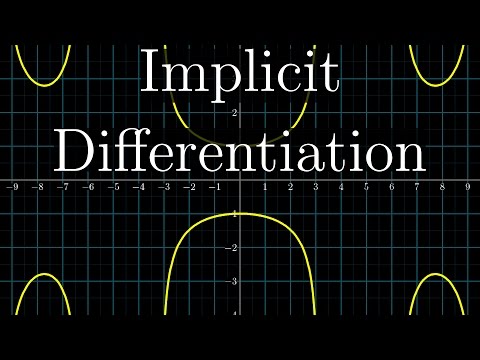
Implicit functions \[x^2 + y^2 = 25 \implies 2x + 2y\frac{dy}{dx} = 0 \implies \frac{dy}{dx}=-\frac{x}{y}\]
Implicit differentiation
Inverse functions \[y=f(x), x=g(y), x=g(f(x)) \implies x'=g'(f(x))\cdot f'(x) \implies \frac{1}{f'(x)}=g'(f(x))\]
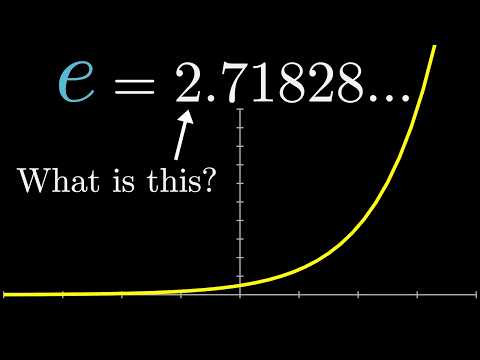
Exponent functions \[y=a^x, y'(x)=\lim_{\Delta x \to 0} \frac{a^{x+\Delta x} - a^x}{\Delta x}=a^x\lim_{\Delta x \to 0} \frac{a^{\Delta x} - 1}{\Delta x}=a^xM(a)\] \(M(a)\) is the slope of the tangent line to \(a^x\) at \(0\). See below. \[M(a)=\lim_{\Delta x \to 0} \frac{a^{\Delta x} - 1}{\Delta x}=\lim_{\Delta x \to 0} \frac{a^{0 + \Delta x} - a^0}{\Delta x}\] The \(a\) at which \(M(a) = 1\) is known as constant \(e\) or Euler’s number. \[\frac{de^x}{dx} = M(e)e^x = 1 \cdot e^x = e^x\]
Euler’s number graphically
Exponential derivatives