Function Approximation
Prerequisites Derivative
Linear approximation
When function is approximated by a linear function it is a linear approximation or linearization of a function. Linear derivative approximation is when we use the derivative of the function at some point to get its linear approximation at the vicinity \(\Delta x\) of the point. The second derivative of function gives us concavity and hence whether the function is located below or above its linear approximation. Also the bigger the second derivative the bendier the curve thus the less is \(\Delta x\) that can be used for the linear approximation.
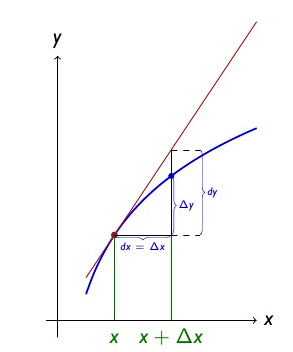 Linear approximation
Linear approximation
Mathematically the linear approximation \(g\) at the point \(a\) is when \(f(a)=g(a), f'(a)=g'(a)\). Let \(x\) be the derivative point: \[\Delta f \approx Slope_{tangent} \Delta x \approx f'(x)\Delta x, \Delta x \to 0\] \[f(x + \Delta x) \approx f'(x)\Delta x + f(x), \Delta x \to 0\]
Approximation of sum The approximation of sum is equal to the sum of approximations.
Approximation near 0 This is quite an important topic. We know some approximations of basic functions near \(0\). \[x \approx 0, (1+x)^r \approx 1+rx,\text{ } sin(x) \approx x,\text{ } e^x \approx 1+x,\text{ } ln(1+x) \approx x\]
Approximation near any point By definition we can approximate a value of function near the point \(a\) as: \[f(x) = f'(a)(x-a) + f(a), x \to a\] It would be hard to apply this if we want to know an approximated value of \(e^x, x \approx 3\). We can use a function composition and an approximation near \(0\) to find it. \[e^x_{x \to 3} = e^{u+3}_{u \to 0} = e^3e^u\]
\[e^3e^u_{u \to 0} \approx e^3(1+u)_{u \to 0} = e^3(1+x-3) = e^3(x-2), x \to 3 \]
We have used a replacement \(x = u + 3, x \to 3 \iff u \to 0\).
Another example. \(sin(x), x \approx 10\pi\) \[sin(x)_{x \to 10\pi} = sin(u + 10\pi)_{u \to 0} = sin(u)cos(10\pi) + sin(10\pi)cos(u), u \to 0\] \[sin(u) \approx x, cos(u) \approx 1, u \to 0\] \[ucos(10\pi) + sin(10\pi) = (x-10\pi)cos(10\pi) + sin(10\pi), x \to 10\pi\]
Approximation of non-linear composition If \(g(0)=0\) then to find an approximation of \(f(g(x))\) near \(0\) we can take a linear approximation for \(f(u)\) and substitute \(g(x)\) in for \(u\). This only works when \(g(0)=0\). \[f(u) \approx f(0) + f'(0)u \implies f(g(x)) \approx f(g(0)) + f'(g(0))g(x)\] Example. \[(1+x^2)^{-1} = (1 + u)^{-1} \approx 1-u = 1-x^2\] We could’ve done the replacement cause \(x \to 0 \iff x^2 \to 0\). Lets find the approximation at \(x=7\) \[(1+x^2)^{-1} = (1 + (u+7)^2)^{-1} = (50+14u+u^2)^{-1} = (50 + v^2)^{-1} \approx \text{…} \]
Another reason why approximations near 0 are important Suppose that you measure the velocity of an object by measuring that it takes \(1\) second to travel \(1.2\) meters. The measurement error is \(.001\) meters in distance, and the error in time is \(.01\) second. What is the absolute value of the error in the linear approximation for the velocity? \[v = \frac{x}{t} \implies v + \Delta v = \frac{x+\Delta x}{t + \Delta t} = (x+\Delta x)(t+\Delta t)^{-1}\] \[=(x+\Delta x)\frac{1}{t}(1+\frac{\Delta t}{t})^{-1}\] Now we use \( (1 + x)^r \approx 1 + rx\) for \(x = \Delta t\) cause \(\Delta t \to 0\) \[v + \Delta v \approx \frac{x}{t}+\frac{\Delta x}{t}-\frac{x\Delta t}{t^2}-\frac{\Delta x \Delta t}{t^2}\] \(\Delta x \Delta t\) can be neglected as it’s quadratic. \[v + \Delta v \approx v+\frac{x}{t}-\frac{x\Delta t}{t^2}\] \[\Delta v \approx \frac{x}{t}-\frac{x\Delta t}{t^2}\]
Quadratic approximation
When function is approximated by a quadratic function it is a quadratic approximation of a function. Graphically it is the best fit parabola to \(f\). Mathematically it is \(f(a)=g(a), f'(a)=g'(a), f''(a)=g''(a)\) where \(g\) is the approximation function. \[x \approx a \implies f(x) \approx f(a) + f'(a)(x-a) + \frac{f''(a)}{2}(x-a)^2\] \[x \approx 0 \implies f(x) \approx f(0) + f'(0)(x) + \frac{f''(0)}{2}(x)^2\]
The polynomial approximation as a consequence: \[x \approx a \implies f(x) \approx \Sigma_{n=0}^{\infty}\frac{f^{(n)}(a)(x-a)^n}{n!} \] \[x \approx 0 \implies f(x) \approx \Sigma_{n=0}^{\infty}\frac{f^{(n)}(0)x^n}{n!}\]
Error approximation notation
\[f(x) = O(g(x)), x \to \infty \iff \exists x_0 \land M > 0, \forall x>x_0 \implies f(x) \leq M|g(x)|\] \[f(x) = O(g(x)), x \to a \iff \exists M > 0 \land \delta > 0, \forall 0<|x-a|<\delta \implies f(x) \leq M|g(x)|\] Example \[(1 + x)^5 \approx 1 + 5x, x \to 0 \text{, linear approximation} \] \[(1 + x)^5 = 1 + 5x + \text{approximation error}, x \to 0 \] \[(1 + x)^5 = 1 + 5x + 10x^2 + 10x^3 + 5x^4 + x^5\] \[\text{approximation error} = 10x^2 + 10x^3 + 5x^4 + x^5\] \[x \to 0 \implies 10x^2 \to 0, 10x^3 \to 0, 5x^4 \to 0, x^5 \to 0 \] \[10x^2 + 10x^3 + 5x^4 + x^5 \leq 10x^2 + x^2 + x^2 + x^2 = 13x^2 = O(x^2)\] \[\text{approximation error} = 13x^2 = O(x^2)\]